补码起源
补码起源于数学计算中的概念,详见 wiki
。wiki 中对于补码的定义是
For a given number of places half of the possible representations of numbers encode the positive numbers, the other half represents their respective additive inverses. The pairs of mutually additive inverse numbers are called complements.
这里主要说一下其中的基数补码
(radix complement)。基数补码的定义是一个 n 位数的 b
进制数字 y 的基数补码为 diminished radix complement
(diminished 是降低,减少的意思),它的定义为
1) 其中
2) 举个例子,比如说
3) 再来个更具体的图 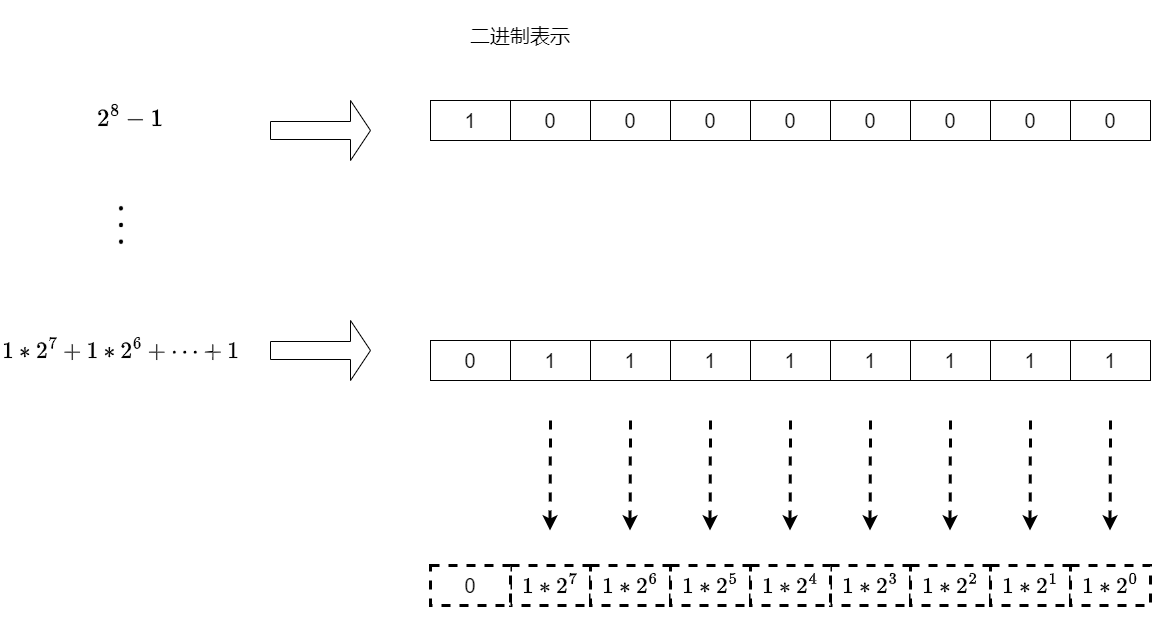
二的补码
1) 咬文嚼字
有了 radix complement
和 diminished radix complement
的概念后,二的补码中的二自然就是 radix 了,也叫作
two's complement 。那 diminished radix
呢?wiki 中的叫法是 ones'
complement。两个叫法中有个微小的差别就是 s 的位置,
第一种补码表示互为补码的数字是基于二进制表示的,而第二种补码很形象的表示出计算补码时
2) 从 0.9 到
1 实现补码
现在我们有了补码的概念和计算方法,那我们先来试着计算一个数的补码吧。比如计算一下
在 8 个 bit -26 如何表示 。首先 -26 是 通过其补码 26
间接算出来的。直接上图。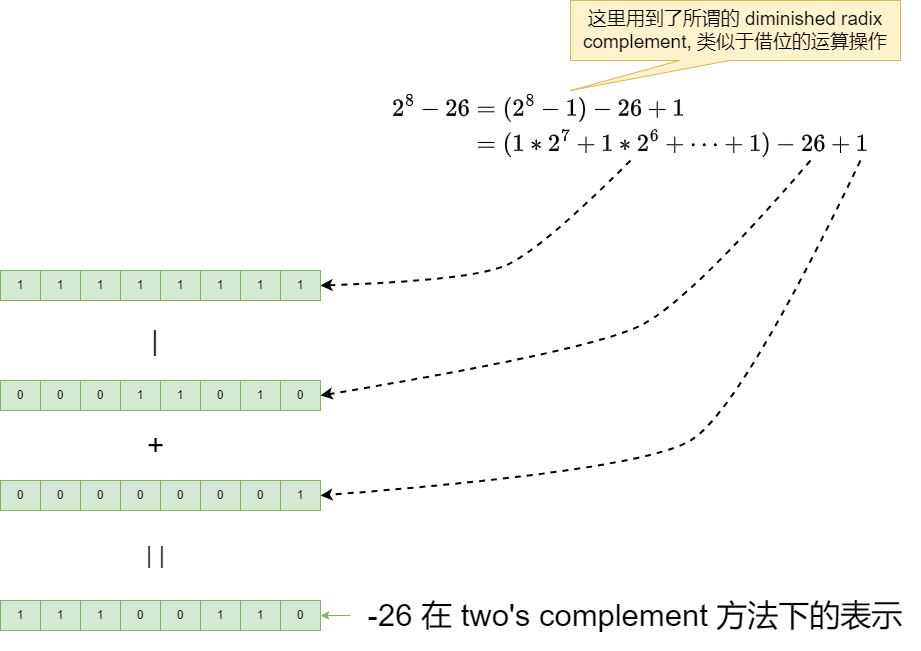
同样的道理,-26 在 8位数 并且 eight's complement
, ten's complement 或 sixteen's complement 下表示都可以这么算。示例如下
因为减去一个数也可以看作是加上一个负数,所以我们这里只考虑加法运算。
- 比如计算 x - y ,我们可以先计算出 -y 的 radix complement(这里假设是
two's complement), 即
4) 补码中的乘除运算
先吐为快
二的补码?补码这玩意和二有什么关系?计算的时候我可一点没看到“二”呀!就因为是二进制数,所以叫二的补码?我还说这数长得像是我家大黄,所以叫大黄的补码呢!好嘛,看了看
wiki ,又看了看学校讲的 (真是给我气吐了)。two's complement
翻译为二的补码(也有叫二的补数),
ones' complement翻译为反码(???)
